[Back to TullyRunners Home Page]

Speed Ratings and Track Times - A Statistical Correlation

 Bill Meylan (April 16, 2007)

Link - Chart of Speed Ratings with Corresponding Times for 1600 Meters & 3200 Meters and 1500 Meters & 3000 Meters ...

** Note ... This Article has UPDATED with newer data which are likely better ... See Updated Chart of XC Speed Ratings with Approximated Times for Various Track Distances

Introduction

Every year I receive inquires concerning the relationship of speed ratings and track times ... Basically, people want to know how to translate a certain track time (such as 3200m or 1600m track time) into a cross country speed rating.  To be honest, the relationship is not that great and is best described by a fairly wide range of values (which may or may not be useful).  With the number of inquiries increasing, I decided to post a formal presentation that describes the relationship in terms of statistics with a resulting chart of corresponding times and speed ratings ... The chart is posted on a separate web-page ... This article describes how the numbers were derived.

The Data

Statistical correlations require data ... This correlation requires corresponding track times and speed ratings ... This data were collected as follows:

(1) Track Times were taken from the on-line track databases as they existed in early April 2007 (Boys Track Database ... Girls Track Database) ... In general, for every boy in the database, his best 3200m and 1600m times were extracted from the past year or two ... A similar data extraction was done for the girls 3000m and 1500m.

(2) Speed Ratings were taken from the existing on-line cross country databases as they existed in early April 2007 ... An "overall" speed rating was derived for every runner with data for the 2006 XC season ... An "overall" speed rating is a composite of the highest speed ratings (both recent and seasonal) and various averages (both recent and seasonal) ... Overall speed ratings are used for the individual XC rankings on this web-site (see NY State Boys Rankings Page as an example).

Note ... The existing on-line databases (as of April 2007) are limited to NY State runners (who have not graduated) ... So the statistical correlation was done strictly with NY State runners.

Correlation Methodology

Four separate correlations were done:

(1) Boys 3200m vs. Speed Rating
(2) Boys 1600m vs. Speed Rating
(3) Girls 3000m vs. Speed Rating
(4) Girls 1500m vs. Speed Rating

For the Boys 3200m vs. Speed Rating correlation, the list of boys with 3200m race times was compared to the list of boys with a 2006 speed rating ... Boys having both a 3200m time and a speed rating had their corresponding 3200m times and speed ratings placed into a statistical spreadsheet program (a total of 559 boys had both) ... The spreadsheet had two columns ... (1) speed ratings and (2) the race time in seconds.

The  two columns in the spreadsheet were used to derive an equation  via a simple linear regression ... A linear regression finds the equation for a straight-line that is a statistical "best-fit" for the data points on a graph (see the correlation graphs below).

The initial linear regression was used to identify outlier data points and remove those data points from the regression ... for example, any data point in the the Boys 3200m vs. Speed Rating correlation that deviated by more than half-a-minute (from the straight-line) was thrown-out ... After removing all outlier data points, the regression was redone.

A similar procedure was done for all four separate correlations ... Graphs (with outliers removed) and statistics for the correlations are shown  below.

Problems

A simple linear regression depends upon data points that are roughly equal in quality ... While many data points in these correlations are roughly equal in quality, there are also a fair number that may not be equal in quality ... And the quality of the resulting correlation depends on the quality of the data ... Here are some possible problems:

(1) The track database has limited data for some runners due to the availability of results ... Therefore, their "best" track times at various distances may not be in the database ... if the difference between the actual best time (not in the database) and the time in the database is small, then the problem is minor ... but sometimes there may be large differences.

(2) Not all runners have representative track times at various distances ... One reason is some runners do not run certain distances in track or only run the distances infrequently or not "all-out" for time.  For example, Geoff King (FM) has a database best 3200m time of 9:51.3 which is clearly not representative of runner with a best 1600m time of 4:16.35 or a Steeplechase of 9:36.0.

Some runners don't get a chance to run a fast competitive time at some distances because a team may have a bunch of good distance runners and only a select few get the opportunity to run that distance ... so a best-time in my track database may be skewed.

As another example, some runners never try to run a fast track time at a specific distance ... Lopez Lomong (Tully) was a Footlocker Finalist and NY State XC Federation champion (and a 4:10 1600m runner), but his best outdoor 3200m in high school was 9:36 because Lopez never attempted to run a fast 3200m (he only ran the distance to score points for the team in certain meets) ... Dominic Luka (Tully), second at NY XC Feds, never ran  a sub-10:00 3200m in high school because he typically ran the 200m to 800m distances in track.

(3) Difficult to quantify, but some runners are just better at track than cross country or vice versa ... One reason is some runners just prefer one season to the other ... Another reason is  the added distance in XC affects some runners more than others.

These problems (and others) can cause some inequalities in the data points used to derive an equation ... removal of outlier data points fixes some of the problem (but not all).

One Fix ... One method to minimize data inequality is to "weight" some data points as better than others ... This can be accomplished by going through the databases and selecting individual runners with lots of good available data for both track and cross country ... Examples are Hannah Davidson (Saratoga) and Tommy Gruenewald (FM) - data for these types of runners can help position the location of the straight line at the upper regions of the data (the top runners have much more data in the track database than other runners).

Results - Accuracy of the Equations

The statistics and graphs of the equations are shown below ... Even with the outlier data points removed, the graphs shown a significant spread (range of data above and below a best-fit straight-line).

For the Boys 3200m (after outlier removal) - the average deviation is 10.58 seconds ... This means that on average, the 3200m time varies by plus or minus 10.58 seconds from a specific speed rating ... That's quite a bit - but not surprising due to the nature of the data ... The R-squared correlation coefficient is 0.775 which basically means that the equation can predict 77.5% of the variance from a perfect-fit (which isn't too bad for this type of data).

Please remember this about the resulting equations ... They may appear to be exact, but they are only a "best-fit" for a data range of values that will vary by a certain margin ... The equations are not perfect - and could never be perfect because the data upon which they are based are not perfect.

A Chart of Speed Ratings vs. Track Times (application of the equations) is located on a separate web-page.

Conclusion

I can say this ... the graphs and statistics demonstrate there is a reasonable statistical correlation between track times and speed ratings ... But it must be remembered there is a range of variation (plus or minus a certain number of seconds) over which the equations are applicable.

Side-Consideration ... The Chart of Speed Ratings vs. Track Times also shows the corresponding times for 3200m vs. 1600m vs. 3000m vs. 1500m ... This correspondence was not done directly by this study; however, the corresponding times have some merit for the following reason - many runners had both a 3200m and 1600m time (or both a 3000m and a 1500m time) ... since the same speed rating was used for both times, a cross-correlation exists which directly relates one distance to the other for these runners.

Statistics and Graph Generation ... All statistics and graphs were done using ProStat v4.11 (Poly Software International) software on a Dell XPS 410 computer (Windows Vista operating system with 2GB memory, E6700 dual-core processor).

Graphs and Statistical Results:

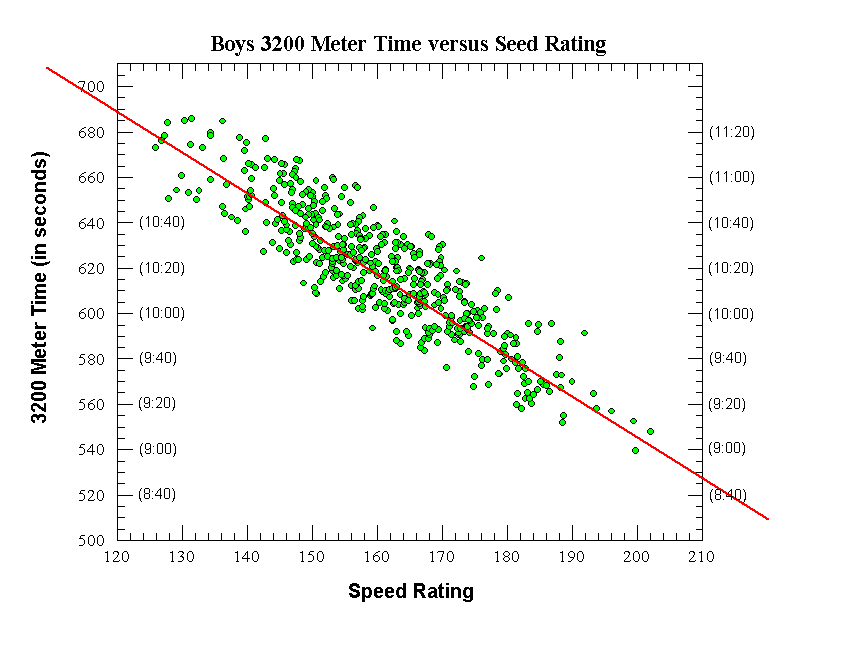Boys 3200 Meters Final Equation (straight red line on graph): 3200m Time (in sec) = -1.775 x Speed Rating + 900 Raw data: Number of data points (individual runners) = 559 Correlation coefficient (r) = 0.812 Correl. coeff. squared (r^2) = 0.659 Standard deviation (seconds) = 16.47 seconds Average deviation (seconds) = 12.73 seconds After Initial removal of outlier data points: Number of data points (individual runners) = 519 Correlation coefficient (r) = 0.8803 Correl. coeff. squared (r^2) = 0.775 Standard deviation (seconds) = 12.87 seconds Average deviation (seconds) = 10.58 seconds

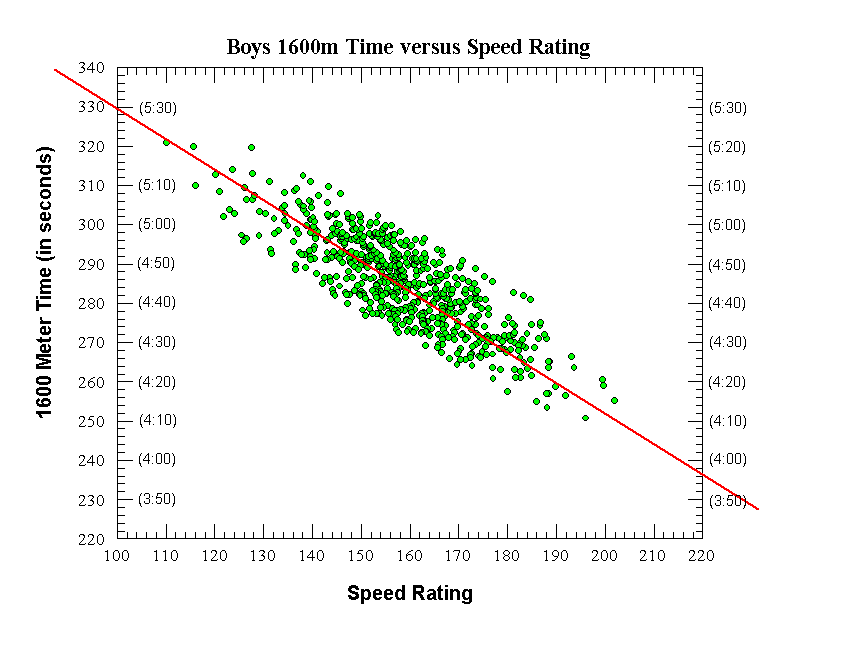Boys 1600 Meters Final Equation (straight red line on graph): 1600m Time (in sec) = -0.7625 x Speed Rating + 405.25 Raw data: Number of data points (individual runners) = 695 Correlation coefficient (r) = 0.7576 Correl. coeff. squared (r^2) = 0.574 Standard deviation (seconds) = 8.32 seconds Average deviation (seconds) = 6.64 seconds After Initial removal of outlier data points: Number of data points (individual runners) = 636 Correlation coefficient (r) = 0.8246 Correl. coeff. squared (r^2) = 0.680 Standard deviation (seconds) = 6.74 seconds Average deviation (seconds) = 5.63 seconds

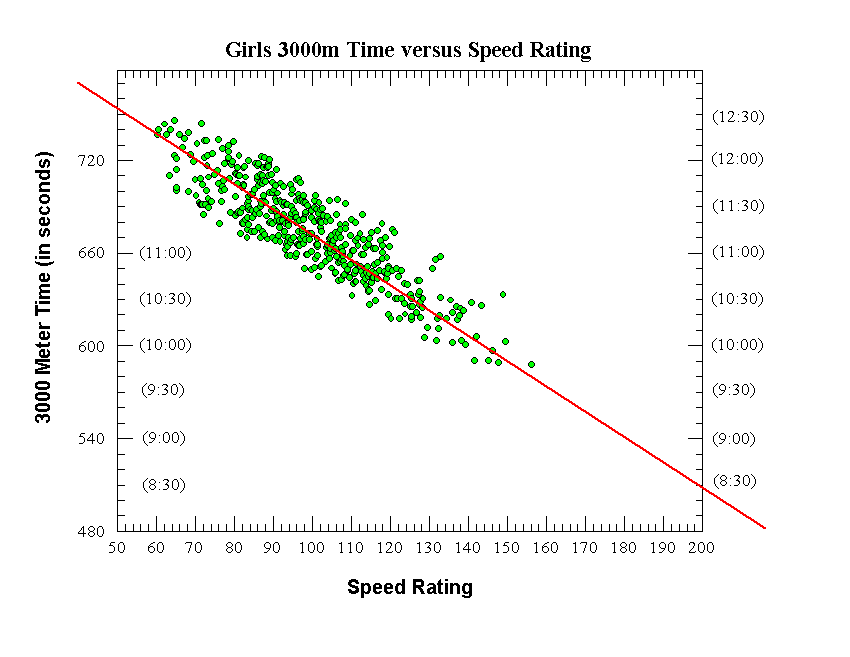Girls 3000 Meters Final Equation (straight red line on graph): 3000m Time (in sec) = -1.6267 x Speed Rating + 834.3 Raw data: Number of data points (individual runners) = 560 Correlation coefficient (r) = 0.7828 Correl. coeff. squared (r^2) = 0.613 Standard deviation (seconds) = 22.5 seconds Average deviation (seconds) = 17.5 seconds After Initial removal of outlier data points: Number of data points (individual runners) = 471 Correlation coefficient (r) = 0.8891 Correl. coeff. squared (r^2) = 0.791 Standard deviation (seconds) = 14.9 seconds Average deviation (seconds) = 12.5 seconds

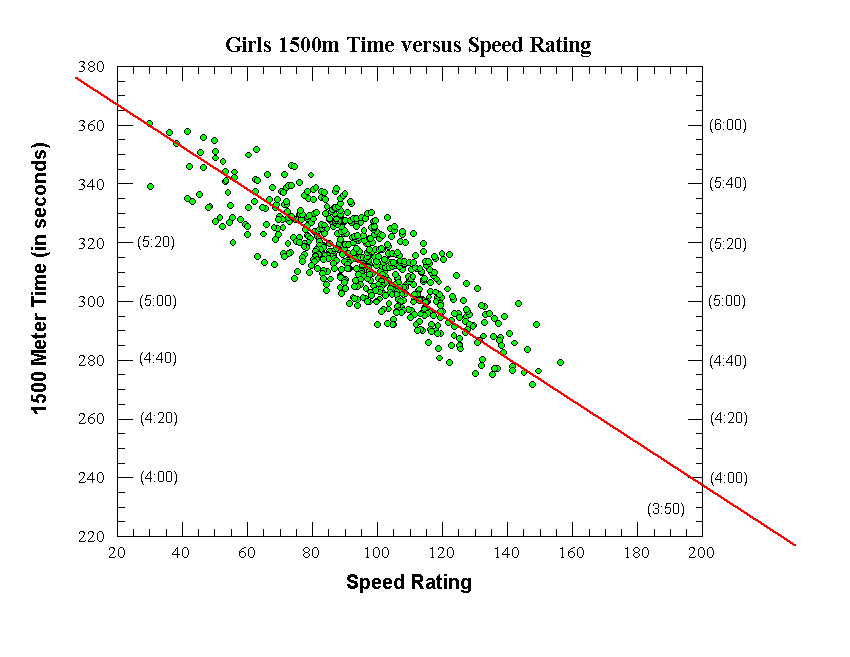Girls 1500 Meters Final Equation (straight red line on graph): 1500m Time (in sec) = -0.733 x Speed Rating + 381.7 Raw data: Number of data points (individual runners) = 672 Correlation coefficient (r) = 0.76 Correl. coeff. squared (r^2) = 0.578 Standard deviation (seconds) = 10.80 seconds Average deviation (seconds) = 8.54 seconds After Initial removal of outlier data points: Number of data points (individual runners) = 625 Correlation coefficient (r) = 0.825 Correl. coeff. squared (r^2) = 0.68 Standard deviation (seconds) = 8.90 seconds Average deviation (seconds) = 7.31 seconds